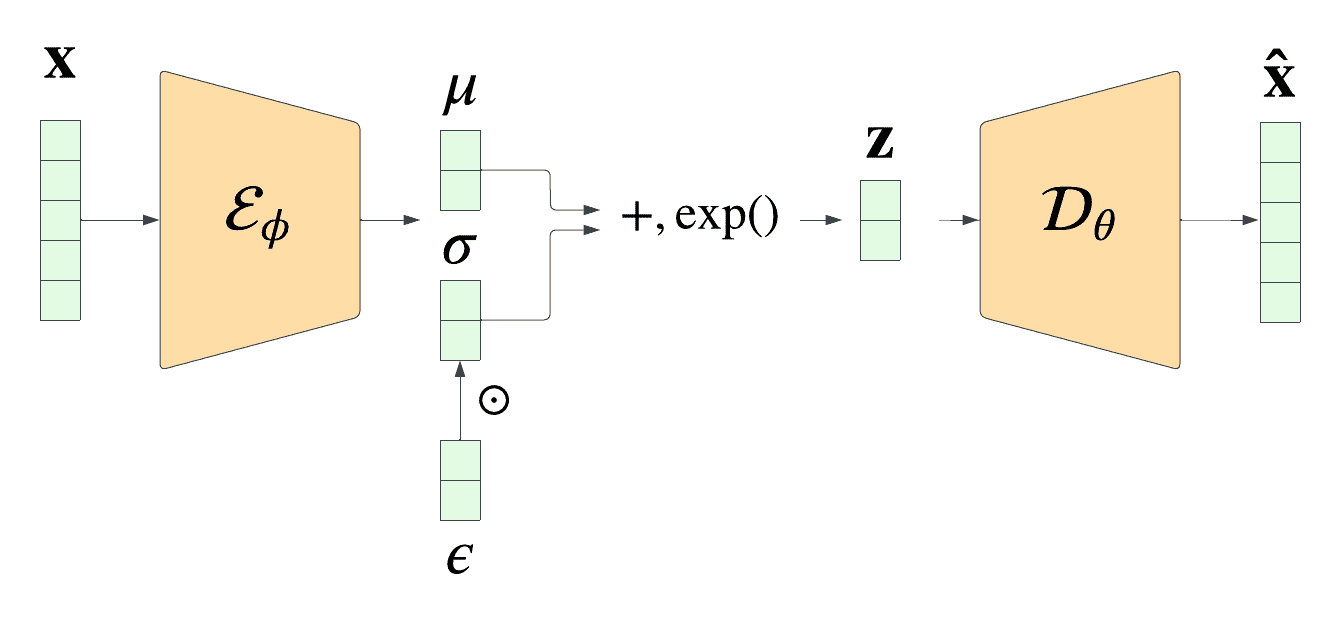
Variational Autoencoder (VAE)

Generative models in machine learning are capable of looking at a set of data points (e.g. images), capturing some inner structure in them and producing new data points (e.g. new images), which bear the properties of the training data set.

Since its inception in the late 2013 Variational Autoencoder (VAE) has become one of two most popular generative models for producing photorealistic images. A popular alternative is called Generative Adversarial Networks (GANs), they are beyond the scope of this post.

To understand the ideas behind VAE, first we need to understand regular autoencoders. To understand motivation for both regular autoencoders and VAE, we need some background in information theory. For understanding VAE we will also cover some background in Bayesian machine learning.

Information theory: entropy, mutual information and KL-divergence

In 1940-1950 information theorists such as Claude Shannon posed a set of problems, related to finding the most economical ways of data transmission.

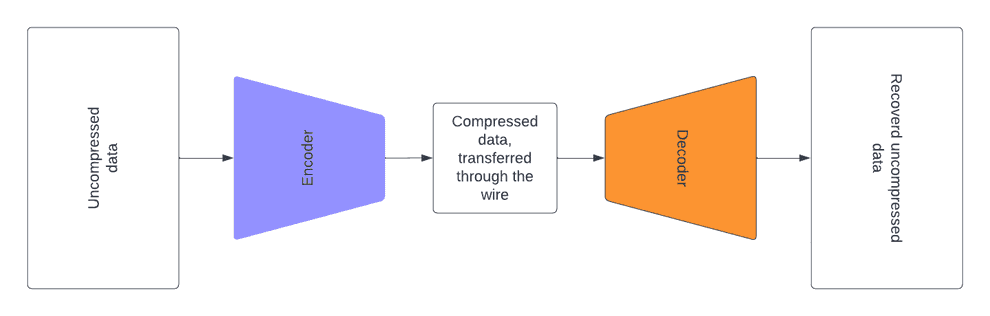
Suppose that you have a signal (e.g. long text in English), and you need to transmit it through a channel (e.g. wire) with a severely limited bandwidth. It would be beneficial to compress this signal, using some kind of encoding, before transfering it through the wire, so that we make as good use of our data transfer channel, as possible. The receiving side should decompress the signal after receiving it.

Suppose that you encode each letter of your alphabet with a sequence of 0s and 1s. What is the optimal way to encode each the letters?

It is intuitive that if you encode frequent letters with the shortest sequences and non-frequent letters with remaining (longer) sequences, you’ll get an optimal encoding. Consider the following example of an alphabet and an optimal encoding:

Observe that the length of the code of letter $A$ equals to $-\log_2 p(A)$.

If your alphabet has a distribution $p$, e.g. $p(A) = 0.5$, the optimal encoding of your signal would achieve the minimal length of average text, if $H(p) = \sum \limits_i p_i \log p_i = \mathbb{E} (-\log p) \to \min$.

$H(p)$ is called entropy, as previously this function was introduced in physical chemistry by Ludwig Boltzmann to describe a different process.

Now, if you use an encoding with a different distribution of letter codes $q$ to transfer your signal, this encoding would be sub-optimal, as average length of a letter would be $\sum \limits_i p_i \log q_i$.

The difference in length between the optimal encoding and sub-optimal encoding is then $D(p, q) = - \sum \limits_i p_i \log q_i - (-\sum \limits_i p_i \log p_i) = - \sum \limits_i p_i \frac{ \log q_i }{ \log p_i }$.

This quantity is called Kullback-Liebler divergence, and for encoding to be optimal it should be minimal. As entropy $H(p) = \sum \limits_i p_i \log p_i$ does not depend on $q$, it would suffice to optimize $H(p,q) = \sum \limits_i p_i \log q_i$, this quantity is known as Cross entropy.

Autoencoders

Inspired by information theory, machine learning practitioners employed the concept of Autoencoders.

To the best of my knowledge first publication of autoencoders or autoassociative neural networks was made by Mark Kramer in 1991, where autoencoders were seen as a non-linear dimensionality reduction tool, a non-linear analogue of PCA.

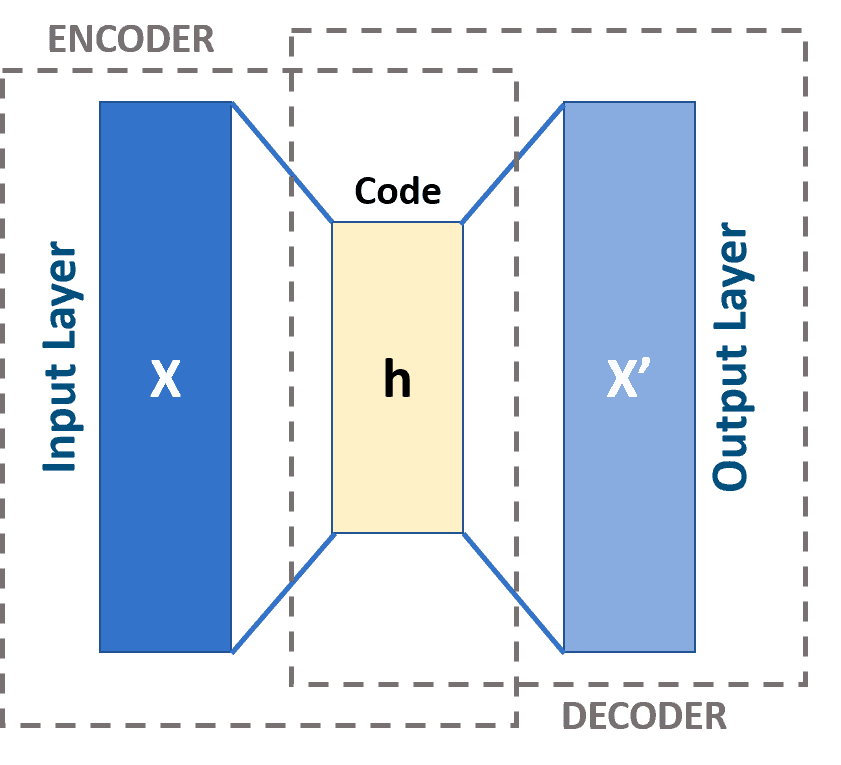
The logic of autoencoder is to train such encoder $\mathcal{E}_{\phi}$ and decoder $\mathcal{D}_{\theta}$ neural networks that encoder can compress the high-dimensional input data $x$ to a low-dimensional latent representation $z$ (or $h$ on the image below) and then the decoder is able to reconstruct $\hat{x}$ (or $x'$ on the image below) accurately enough from this latent representation.

This approach was re-used much later, circa 2010, by Yoshua Bengio group. They figured out that autoencoders can be used for other purposes, such as denoising:

Moreover, Bengio borrowed the idea of stacking individual encoders/decoders from Hinton’s RBMs and this approach gave rise to stacked denoising autoencoders and, eventually, Diffusion models, but that’s a topic for another day.

Holes in the latent space

Now, what happens, if we drop the decoder part, just sample a random point from the encoder latent space and generate an output from it with the decoder? This is supposed to produce us an image. Hence, our model would be generative.

However, one of the obvious problems that arises is the fact that training data points oftentimes do not cover the whole latent space. In the worst-case scenario theoretically our autoencoder could just map all the data points to a straight line, effectively enumerating them.

Thus, if we wanted to generate an image and sampled a point from the latent space that belongs to a hole, we won’t get a valid output. So, we face a problem: we have to come up with a way to regularize our latent space, so that the whole manifold of images is mapped to the whole latent space, preferably in a smooth way. This is the motivation for VAE.

VAE makes sure that the latent space has a Gaussian distribution, so that by gradually moving from one point of latent space to its neighbour, we get a meaningful gradually changing output:

Variational autoencoder (VAE)

VAE, devised by Max Welling group in the late 2013, has arguably become the most wide-spread flavour of autoencoders. It maps the data points to a distribution (usually, Gaussian), so that the mapping is smooth and no holes are produced. It is formulated in Bayesian terms.

The idea of this approach starts from the information theory perspective: we want to train such an encoder neural network $\mathcal{E}_{\phi}$ with parameters $\phi$ that the Kullback-Liebler divergence between the input image $\bf x$ and its latent representation $\bf z$ is minimized: $KL({\bf x}, {\bf z}) \to min$.

This principle is also known as Infomax and was borrowed by Bengio and, later, Welling teams from one of the flavours of Independent Component Analysis (ICA).

Computationally VAE minimizes the divergence using stochastic gradient descent. However, as we’ll see later using a regular neural network training approach does not get the job done, as normal gradient estimator has a very high variance and does not converge computationally (we’ll see this in a moment).

Hence, training VAE employs a specific computational technique, called doubly-stochastic gradient descent and a special trick, called re-parametrization trick, which we will explore later.

But first we need to understand the language, in which VAE is described, as it is a Bayesian model, and we will have to cover a lot of background in Bayesian ML.

Bayes formula

To explain the Bayesian framework, employed by VAE, we have to start with Bayes formula:

$\underbrace{ p(z | x) }_\text{posterior} = \frac{ \overbrace{ p(x | z)}^\text{evidence} \cdot \overbrace{p(z)}^{prior} }{ \underbrace{ p(x) }_\text{evidence} }$

In case of VAE the notation is as follows:

• we have a dataset of images $X = \{ {\bf x^{(i)}} \}$
• each input image is denoted $\bf x^{(i)}$
• its latent representation, which is generated by VAE’s encoder half, is denoted $\bf z^{(i)}$
• the weights of encoder network $\mathcal{E}$ are denoted $\phi$; Kingma and Welling call them variational parameters
• the weights of decoder network $\mathcal{D}$ are denoted $\theta$; Kingma and Welling call them generative parameters

The authors of VAE, D. Kingma and M. Welling, assume that there exists some prior distribution of latent parameters $p({\bf z})$, from which latent representation of each data point is sampled. For each image ${\bf x}$ we maximize the posterior $p_{\phi}(z|x)$.

Variational inference

Direct calculation of posterior $p({\bf z} | {\bf x})$ using Bayes formula is impossible, as we need to calculate the probability of evidence $p(x)$, for which the integral $p({\bf x}) = \int p({\bf x} | {\bf z}) p({\bf z}) d {\bf z}$ is intractable (i.e. it is not possible to calculate it analytically or computationally in practice).

So we need to come up with a practical way of overcoming this obstacle.

Typically, Bayesians have two solutions for problems like this: one solution is Markov Chain Monte Carlo methods. In this particular case MCMC estimator is time-consuming and gradient, calculated with it, has a high variance, so the model fails to converge.

An alternative approach is Variational Inference approach, which we explain here.

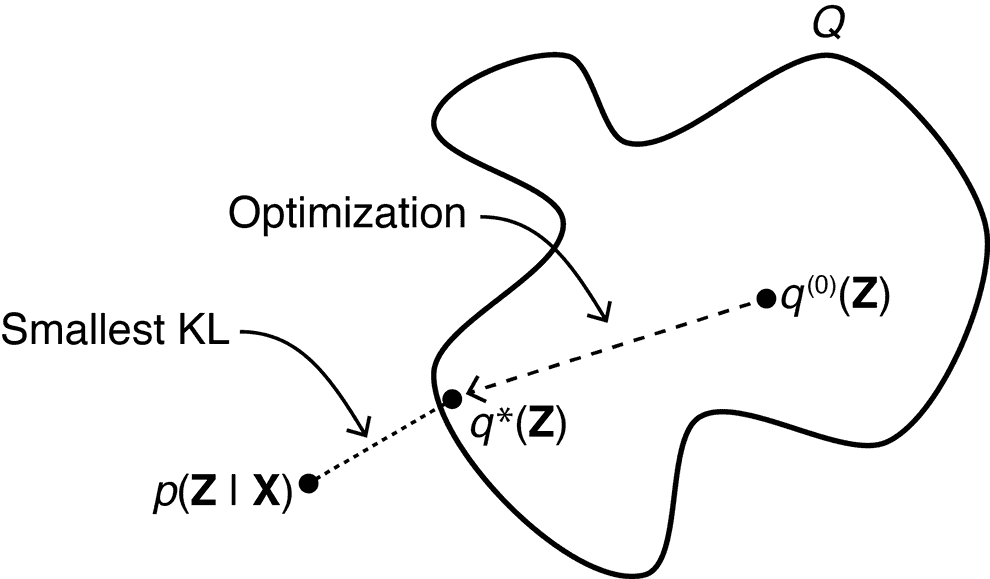
In variational inference we choose a class of functions $Q$, from which we will try to pick an approximation $q({\bf z})$ (called guide) of the posterior $p({\bf z} | {\bf x})$, such that Kullback-Liebler divergence between this approximation and true posterior is minimal.

ELBO maximization

Now, we need to come up with a technical way to find this optimal guide $q({\bf z})$ numerically.

Out of blue sky we consider $\log p(x)$. Let us do 2 tricks with it, first represent it as an integral, and then split it into 2 terms:

$\log p({\bf x}) = \int q({\bf z}) \log{p(x)} d{\bf z} = \int q({\bf z}) \log \frac{p({\bf x}, {\bf z})}{p({\bf z} | {\bf x})} d {\bf z} = \int q({\bf z}) \log \frac{p({\bf x}, {\bf z}) q({\bf z})}{p( {\bf z} | {\bf x} ) q({\bf z})} d{\bf z} =$

$= \int q({\bf z}) \log \frac{p({\bf x}, {\bf z})}{q({\bf z})} d{\bf z} + \int q({\bf z}) \log \frac{q({\bf z})}{p({\bf z} | {\bf x})} d {\bf z} = \mathcal{L}(q({\bf z})) + KL(q({\bf z}) \Vert p({\bf z} | {\bf x}))$.

Now we see that log-evidence $\log p({\bf x})$ consists of two non-negative terms. Let us interpret them:

$\log p({\bf x}) = \underbrace{ \mathcal{L}(q({\bf z})) }_\text{ELBO - Evidence lower bound} + KL(q({\bf z}) \Vert p({\bf z} | {\bf x}))$

The first term is called Evidence Lower BOund (ELBO). The second term is our cost function $KL(q({\bf z}) \Vert p({\bf z} | {\bf x}))$, which Variational Inference aims to minimize. As log-evidence $\log p({\bf x})$ is fixed, the greater ELBO gets, the closer in terms of KL divergence guide $q({\bf z})$ approximates the posterior $p({\bf z} | {\bf x})$:

$KL \ge 0 \Rightarrow KL(q({\bf z}) \Vert p({\bf z} | {\bf x})) \to \min \Leftrightarrow \mathcal{L}(q({\bf z})) \to \max$

Hence, to find the optimal guide $q({\bf z})$, in practice we have to maximize ELBO. Let us break it down further:

$\mathcal{L}(q({\bf z})) = \int q({\bf z}) \log \frac{p({\bf x}, {\bf z})}{q({\bf z})} d{\bf z} = \int q({\bf z}) \log \frac{ p({\bf x}|{\bf z}) p({\bf z}) }{q({\bf z})} d{\bf z} =$

$= \int q({\bf z}) \log p({\bf x}, {\bf z}) d{\bf z} + \int q({\bf z}) \log \frac{ p({\bf z}) }{q({\bf z})} d{\bf z} = \underbrace{ \mathbb{E}_{ q({\bf z}) } \log p({\bf x}|{\bf z}) }_\text{Expected log-likelihood} - \underbrace{ KL(q({\bf z}) \Vert p({\bf z}))}_\text{Regulariser term KL-divergence}$

We see that our loss function consists of 2 terms. The first term characterizes the quality of reconstruction of image from its latent representation. The second term is a regularizer term that guarantees that our guide (i.e. latent space) distribution stays relatively close to the prior $p({\bf z})$, which is usually chosen to be Gaussian.

VAE makes use of ELBO as its loss function for training. It approximates its true gradient with stochastic gradients over mini-batches of data points (e.g. images), so that integrals are replaced with sums.

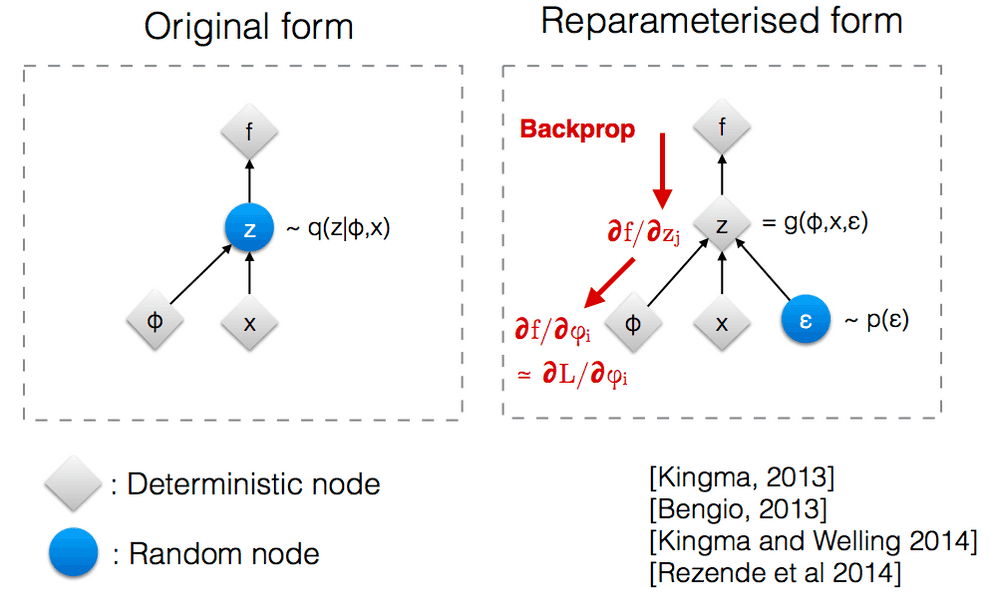
There is also one nitpick: in VAE our latent representation vector $\bf z$ is not deterministic, but stochastic. Hence, in order to make the gradient of ELBO differentiable, we’ll have to use a special reparametrization trick.

Reparametrization trick

Unlike the normal convolutional neural networks, VAE makes use of doubly stochastic gradient descent. Input images are the first source of stochasticity in VAE.

But there is also a second source: in case of VAE the latent representation $\bf z$ is not just a deterministic low-dimensional vector like in normal autoencoders. Instead, it is a random variable (usually, multivariate gaussian), whose mean $\bf \mu$ and variance $\bf \sigma$ the model aims to learn.

So the mean and variance of $\bf z$ are deterministic, but then for each data point in the training batch we sample a random point from that distribution, introducing some extra noise.

Why doing so?

There are 3 reasons, all technical.

First, as I mentioned previously, it is a practical way to achieve a gradient estimator that would actually converge. MCMC gradient estimator, used normally, would have too big of a variance, and training process fails to converge in practice.

Second, we need the parameters $\bf \mu$ and $\bf \sigma$ to be differentiable in order to learn them via error backpropagation. Randomness wouldn’t be differentiable, but if we keep them deterministic, and inject randomness with a separate variable $\epsilon$, it keeps $\bf \mu$ and $\bf \sigma$ differentiable and lets the model learn them.

Third, the data points in the training set might not cover the whole latent space. Randomness helps to partially mitigate the issue of presense of holes in the latent space.

Practical implementation of loss and its gradients

Ok, now we’re done with Bayesian theory. It might by nice for drawing inspiration, but it is “more like guidelines, rather than actual rules”. Time to implement our loss and its gradient it in practice. Look at the loss function again:

$\mathcal{L}(q({\bf z})) = \underbrace{ \mathbb{E}_{ q({\bf z}) } \log p({\bf x}|{\bf z}) }_\text{Expected log-likelihood} - \underbrace{ KL(q({\bf z}) \Vert p({\bf z}))}_\text{Regulariser term KL-divergence}$

First, let us interpret the terms. In case of VAE, our guide $q({\bf z})$ is the output of encoder neural network. As encoder output depends on variational parameters $\phi$ and input data $\bf x$, we will denote $q({\bf z})$ in case of VAE $q_\phi({\bf z} | {\bf x})$. We are searching for the guide in the form of a multivariate Gaussian: $q_{\phi}({\bf z} | {\bf x}) = \mathcal{N}(\bf{z}; {\bf \mu}, {\bf \sigma})$.

Second, $p({\bf x}|{\bf z})$ corresponds to reconstruction of image from the latent representation by the decoder, so it is rather $p({\bf \hat{x}}|{\bf z})$; the term also depends on the decoder (generative) parameters $\theta$, thus we shall denote it $p_{\theta}({\bf \hat{x}}|{\bf z})$. Possible options for it are Bernoulli MLP and Gaussian MLP errors. I’d go with Gaussian - in that case reconstruction error takes the form of L2 error: $\log p({\bf x} | {\bf \hat{x}}) = \log e^{- \frac{({\bf x} - \bf \hat{x})^2}{2} } = ||{\bf x} - {\bf \hat{x}}||^2_2$.

Third, $p({\bf z})$ is a prior of latent representation, again, parametrized on variational (encoder) parameters $\theta$. Prior is often assumed to be Gaussian with zero mean and identity matrix of variance: $p({\bf z}) = \mathcal{N}({\bf z}; {\bf 0}, {\bf I})$

So, we get:

$\mathcal{L}(q({\bf z})) = \int \int \log p_{\theta}({\bf x} | {\bf z}) q_{\phi}({\bf z} | {\bf x}) d{\bf z} d{\bf x} + \int \int q_{\phi}({\bf z} | {\bf x}) \log \frac{p_{\theta}({\bf z})}{q_{\phi}({\bf z} | {\bf x})} d{\bf z} d{\bf x} =$

$= \int \int \log p_{\theta}({\bf x} | {\bf z}) q_{\phi}({\bf z} | {\bf x}) d{\bf z} d{\bf x} + \int \int q_{\phi}({\bf z} | {\bf x}) \log p_{\theta}({\bf z}) d{\bf z} d{\bf x} - \int \int q_{\phi}({\bf z} | {\bf x}) \log q_{\phi}({\bf z} | {\bf x}) d{\bf z} d{\bf x}$.

Let us work with individual terms:

1. $\int \int \log p_{\theta}({\bf x} | {\bf z}) q_{\phi}({\bf z} | {\bf x}) d{\bf z} d{\bf x}$ - this term depends on the choice of reconstruction error function. In case of Gaussian posterior it will look like an L2 norm, in case of Bernoulli - like cross-entropy.

2. $\int \int q_{\phi}({\bf z} | {\bf x}) \log p_{\theta}({\bf z}) d{\bf z} d{\bf x} = \int \mathcal{N}({\bf z}; {\bf \mu}, {\bf \sigma}) \log \mathcal{N}({\bf z}; {\bf 0}, {\bf I}) = -\frac{J}{2} \log(2\pi) - \frac{1}{2} \sum \limits_{j=1}^J (\mu_j^2 + \sigma_j^2)$

3. $\int \int q_{\phi}({\bf z} | {\bf x}) \log q_{\phi}({\bf z} | {\bf x}) d{\bf z} d{\bf x} = \int \mathcal{N}({\bf z}; {\bf \mu}, {\bf \sigma}) \log \mathcal{N}({\bf z}; {\bf \mu}, {\bf \sigma}) = - \frac{J}{2} \log(2\pi) - \frac{1}{2} \sum \limits_{j=1}^J (1 + \log \sigma_j^2)$

In practice we are working with finite sets of points and are using Monte-Carlo estimators. Hence, adding the three terms together and replacing integrals with sums we get:

$\mathcal{L} (\theta;\phi;x^{i})\backsimeq \underbrace{ \frac{1}{2} \cdot \sum \limits_{j=1}^J(1 + 2\log\sigma^i_j-(\mu^i)^2 - (\sigma^i)^2) }_\text{regularization term} + \underbrace{ \frac{1}{L}\sum \limits_{l=1}^L \log p_\theta(x^i|z^{i,l}) }_\text{reconstruction quality term}$.

As I said before, in practice reconstruction quality term takes form of either L2 norm of difference between input and reconstructed image in case of Gaussian posterior $p_{\theta}({\bf x} | {\bf z})$, or cross-entropy in case of multivariate Bernoulli posterior $p_{\theta}({\bf x} | {\bf z})$.

Problems and improvements of VAE

Fuzzy results

Another issue is the fact that output images, generated by VAE decoder, are oftentimes blurred.

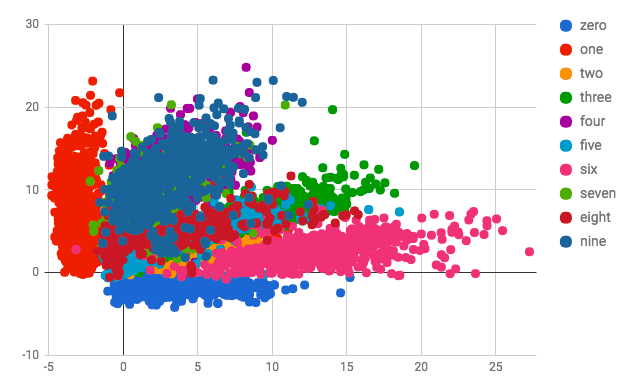
How to explain this phenomenon? Consider latent space of a VAE, trained to recognized MNIST digits:

Some classes (e.g. fours and nines) intersect with each other. If you sample a point from a region of latent space, where both fours and nines are frequent, VAE would basically produce a superposition of nine and four. This results in such a blurry image.

Posterior collapse

There are plenty of other issues left with regularization of the latent space of VAE.

For instance, sometimes generative part of VAE almost ignores the input image and generates a very generic image, very dissimilar from the input. Some authors claim that this happens when the regularization term of VAE (that moves prior on $\bf z$ closer to Gaussian) takes over the reconstruction term. Basically, reconstruction term conflicts with regularization term, and if regularization term wins, input image is ignored by VAE to a significant extent.

Another reason, possibly contributing to the posterior collapse, is the fact that variance of the Gaussian distribution, used in VAE, is diagonal, while in the real distribution the coordinates might not be independent.

This gave rise to dozens of flavours of VAE, which address these and other issues, such as beta VAE, vector quantization VAE (VQ-VAE) and other, which I won’t cover here.

References:

Autoencoders:

• https://en.wikipedia.org/wiki/Autoencoder - wikipedia on Autoencoder
• https://www.jmlr.org/papers/volume11/vincent10a/vincent10a.pdf - stacked denoising autoencoders by Y.Bengio group
• https://www.researchgate.net/profile/Abir_Alobaid/post/To_learn_a_probability_density_function_by_using_neural_network_can_we_first_estimate_density_using_nonparametric_methods_then_train_the_network/attachment/59d6450279197b80779a031e/AS:451263696510979@1484601057779/download/NL+PCA+by+using+ANN.pdf
• https://cedar.buffalo.edu/~srihari/CSE676/14.2%20Denoising%20Autoencoders.pdf - presentation on denoising autoencoders
• https://www.researchgate.net/publication/272086159_Static_hand_gesture_recognition_using_stacked_Denoising_Sparse_Autoencoders
• https://arxiv.org/pdf/1511.06406.pdf - denoising VAE (DVAE) by Y. Bengio et al.

Bayesian ML, VAE and variants:

• https://www.stats.ox.ac.uk/~teh/research/compstats/WelTeh2011a.pdf - Bayesian Learning in Stochastic Gradient Langevin Dynamics by M.Welling, Y.W.Teh
• https://gregorygundersen.com/blog/2021/04/16/variational-inference/ - Gregory Gundersen on Variational Inference (VI)
• https://gregorygundersen.com/blog/2019/11/10/em/ - Gregory Gunderson on Variational EM
• https://towardsdatascience.com/difference-between-autoencoder-ae-and-variational-autoencoder-vae-ed7be1c038f2 - blog post by Aqeel Anwar on VAE with good images
• https://chrischoy.github.io/research/Expectation-Maximization-and-Variational-Inference/ - blog post on VI and Variational EM
• https://www.youtube.com/watch?v=xH1mBw3tb_c - 2019 lecture by D. Vetrov on variational inference
• https://arxiv.org/pdf/1312.6114.pdf - VAE paper by D. Kingma and M. Welling
• https://www.youtube.com/watch?v=9zKuYvjFFS8 - video on AE and VAEs
• https://arxiv.org/pdf/1606.05328.pdf - pixelCNN encoder paper
• https://arxiv.org/pdf/1711.00937.pdf - VQ-VAE paper
• https://arxiv.org/pdf/1812.02833.pdf - disentanglement in VAE paper
• https://arxiv.org/pdf/2110.03318.pdf - on detecting holes in VAE latent space
• https://pyro.ai/examples/svi_part_i.html - implementations of Stochastic VI, VAE etc. in Pyro library
• https://ai.stackexchange.com/questions/8885/why-is-the-variational-auto-encoders-output-blurred-while-gans-output-is-crisp - on blurred outputs of VAE
• https://datascience.stackexchange.com/questions/48962/what-is-posterior-collapse-phenomenon - on posterior collapse
• https://stats.stackexchange.com/questions/347378/variational-autoencoder-why-reconstruction-term-is-same-to-square-loss - on practical aspects of VAE loss
• https://openreview.net/pdf?id=r1xaVLUYuE - Posterior Collapse in VAE paper
• https://www.youtube.com/watch?v=oHtqlRIsXcQ - a talk on Posterior Collapse by the same author as the paper above
• https://www.robots.ox.ac.uk/~cvrg/hilary2006/ppca.pdf - on pPCA (used to understand posterior collapse)
• https://www.tensorflow.org/probability/examples/Probabilistic_PCA - Tensorflow pPCA tutorial
• https://arxiv.org/pdf/1907.06845.pdf - on Bernoulli posterior in VAE

Written by Boris Burkov who lives in Moscow, Russia, loves to take part in development of cutting-edge technologies, reflects on how the world works and admires the giants of the past. You can follow me in Telegram