Optimizers in deep learning
 February 28, 2024 13 min read

In this post I briefly describe the concepts beside the most popular optimizer algorithms in deep learning. I cover SGD, RMSprop, AdaGrad, Adam, AdamW, AMSGrad etc.

Gradient boosting machines 101
 December 31, 2023 6 min read

Gradient boosting machines have been the most efficient method for working with tabular data for the last 10 years. In this post I am going to discuss flavours of GBMs, which originated in these years, their quirks and use cases.

Conjugate gradients
 September 21, 2023 27 min read

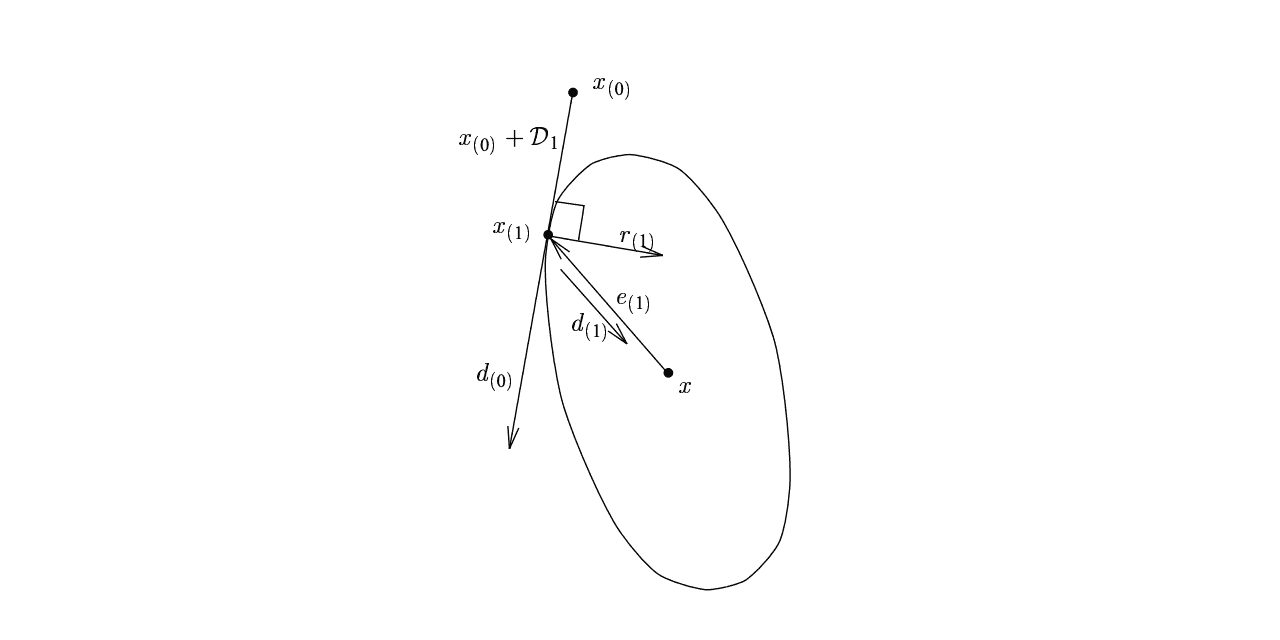
Conjugate gradients is one of the most popular computationally effective methods, used to solve systems of linear equations. Along with other Krylov space methods it can also be used for finding eigenvalues and eigenvectors of a matrix.

Intro to the Extreme Value Theory and Extreme Value Distribution
 April 30, 2023 165 min read

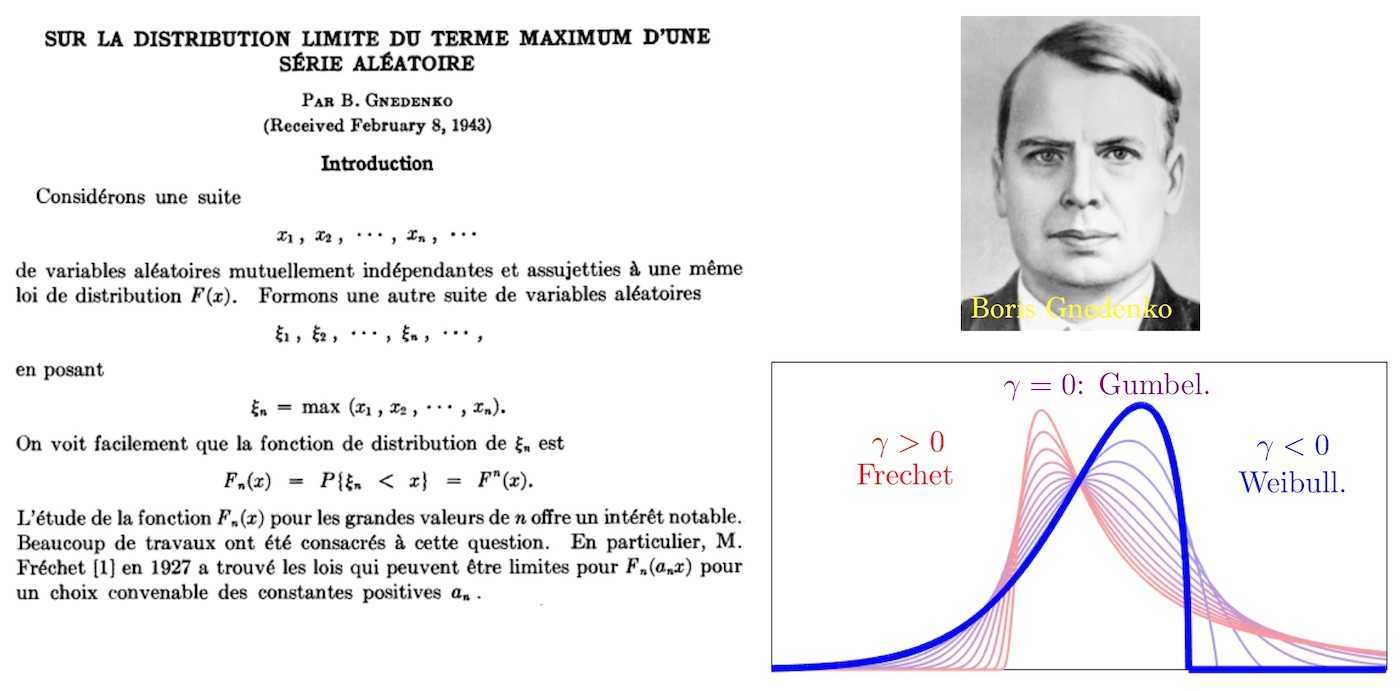
Quite often in mathematical statistics I run into Extreme Value Distribution - an analogue of Central Limit Theorem, which describes the distribution of maximum/minimum, observed in a series of i.i.d random variable tosses. This is an introductory text with the basic concepts and proofs of results from extreme value theory, such as Generalized Extreme Value and Pareto distributions, Fisher-Tippett-Gnedenko theorem, von Mises conditions, Pickands-Balkema-de Haan theorem and their applications.

Variational Autoencoder (VAE)
 December 31, 2022 27 min read

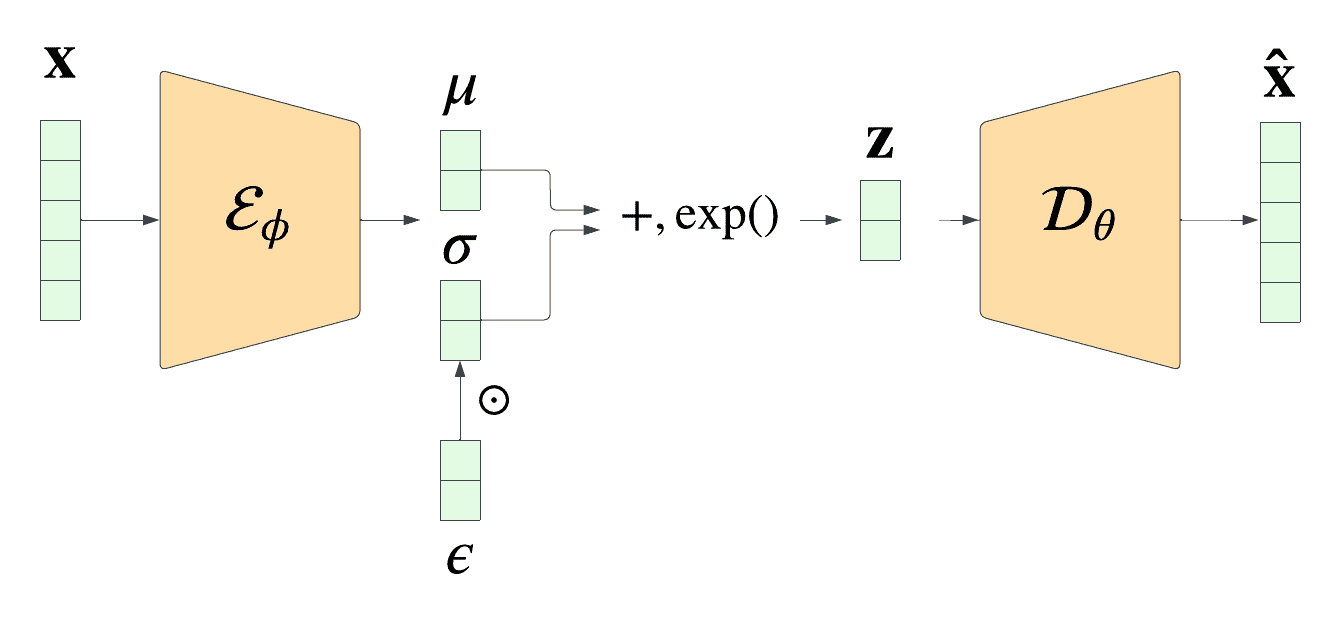
Here I discuss one of the two most popular classes of generative models for creating images.

MDS, Isomap, LLE, Spectral embedding
 December 10, 2022 32 min read

In this post I investigate the multi-dimensional scaling algorithm and its manifold structure-aware flavours.

Economic Complexity Index (ECI)
 November 11, 2022 12 min read

The death of globalism in 2022 brings all kinds of economic sanctions. Lately I've been running into the term Economic Complexity Index (ECI), which reflects the diversification of exports of a country. In this post I investigate the mathematics behind it and draw connections to the problems of Ncut, biclustering etc.

Correspondence between symmetric NMF, k-means, biclustering and spectral clustering
 August 31, 2022 38 min read

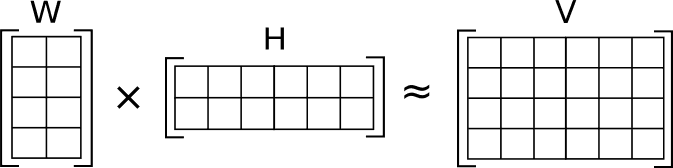
Non-negative matrix factorization (NMF) is the most fashionable method of matrix decomposition among productive, but mathematically illiterate biology students, much more popular than PCA due to its perceived simplicity. However, if you start digging deeper, it happens to have profound connections to a multitude of other techniques from linear algebra and matrix analysis. In this post I discuss those connections.

Intro to compressed sensing
 June 21, 2022 35 min read

For almost a century the field of signal processing existed in the paradigm of Nyquist-Shannon theorem (also known as Kotelnikov theorem in Russian literature) that claimed that you cannot extract more than n Fourier harmonics from a signal, if you have n measurements. However, thanks to the results in functional analysis from 1980s, such as Lindenstrauss-Johnson lemma and Kashin-Garnaev-Gluskin inequality, it became evident, that you can do with as few as log(n)! After application of the L1-norm machinery developed in 1990s, such as LASSO and LARS, a new groundbreaking theory of compressed sensing emerged in mid-2000s to early 2010s. In this post I'll briefly cover some of its ideas and results.

Lagrange multipliers and duality
 May 10, 2022 6 min read

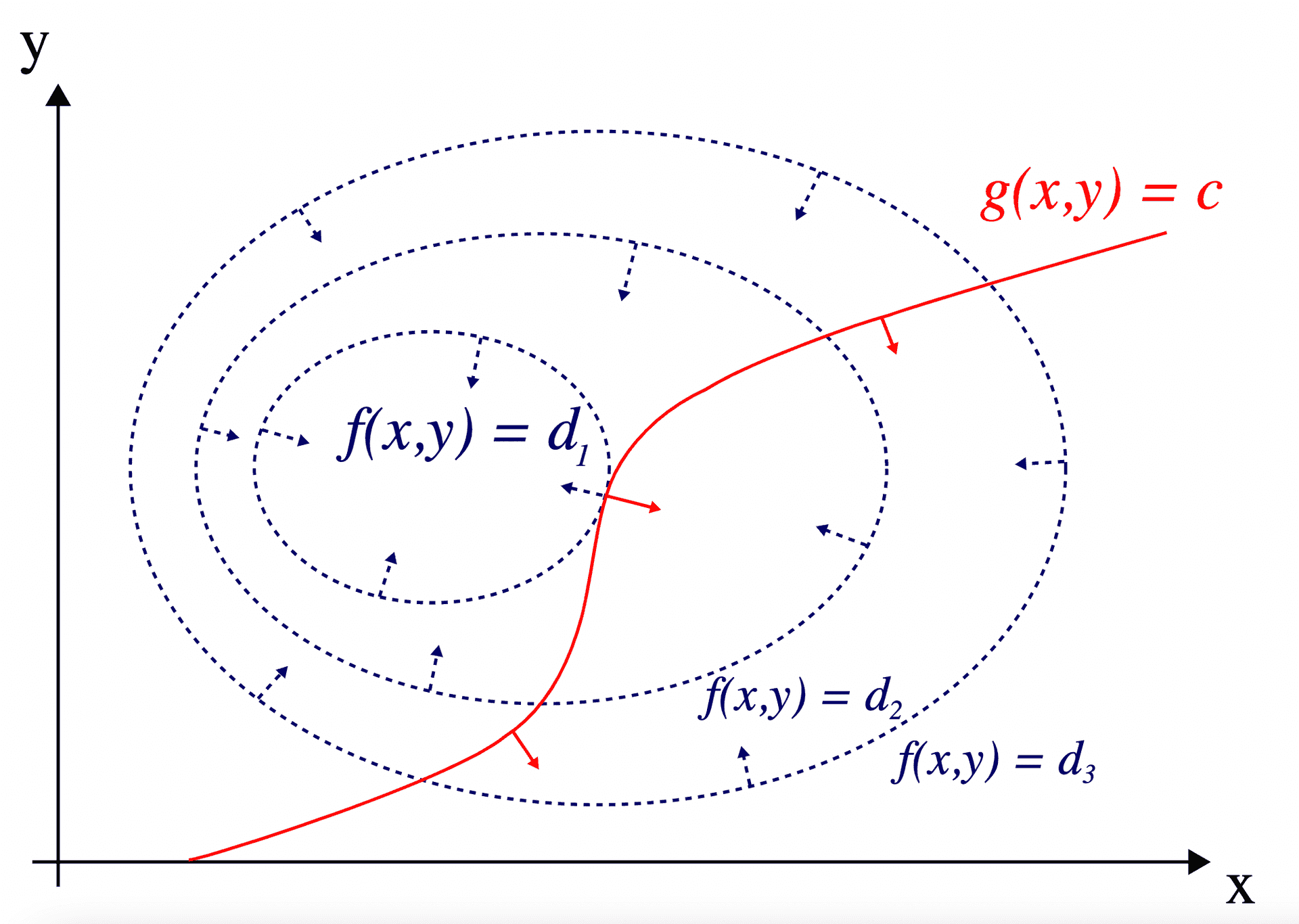
Lagrange multipliers are ubiquitous in optimization theory and natural sciences, such as mechanics and statistical physics. Here I work out its intuition and derivation.

Manim (3blue1brown library for math animations) basics
 February 20, 2022 2 min read

A long time ago I had a dream of a website, where mathematicians could exchange their ideas in a visual form, not as "canned" formulae. At that point I was basically broke and did not have enough money/passion to create a decent library myself. Years later a friend of mine showed me 3blue1brown youtube channel, where a guy was creating beautiful understandable videos about mathematics (shame that I already learnt everything they taught, though). Recently I found out that he actually open-sourced the library he created for making those animation. This post is about it.

Lasso regression implementation analysis
 February 15, 2022 12 min read

Lasso regression algorithm implementation is not as trivial as it might seem. In this post I investigate the exact algorithm, implemented in Scikit-learn, as well as its later improvements.

Modern Portfolio Theory... and Practice
 January 15, 2022 15 min read

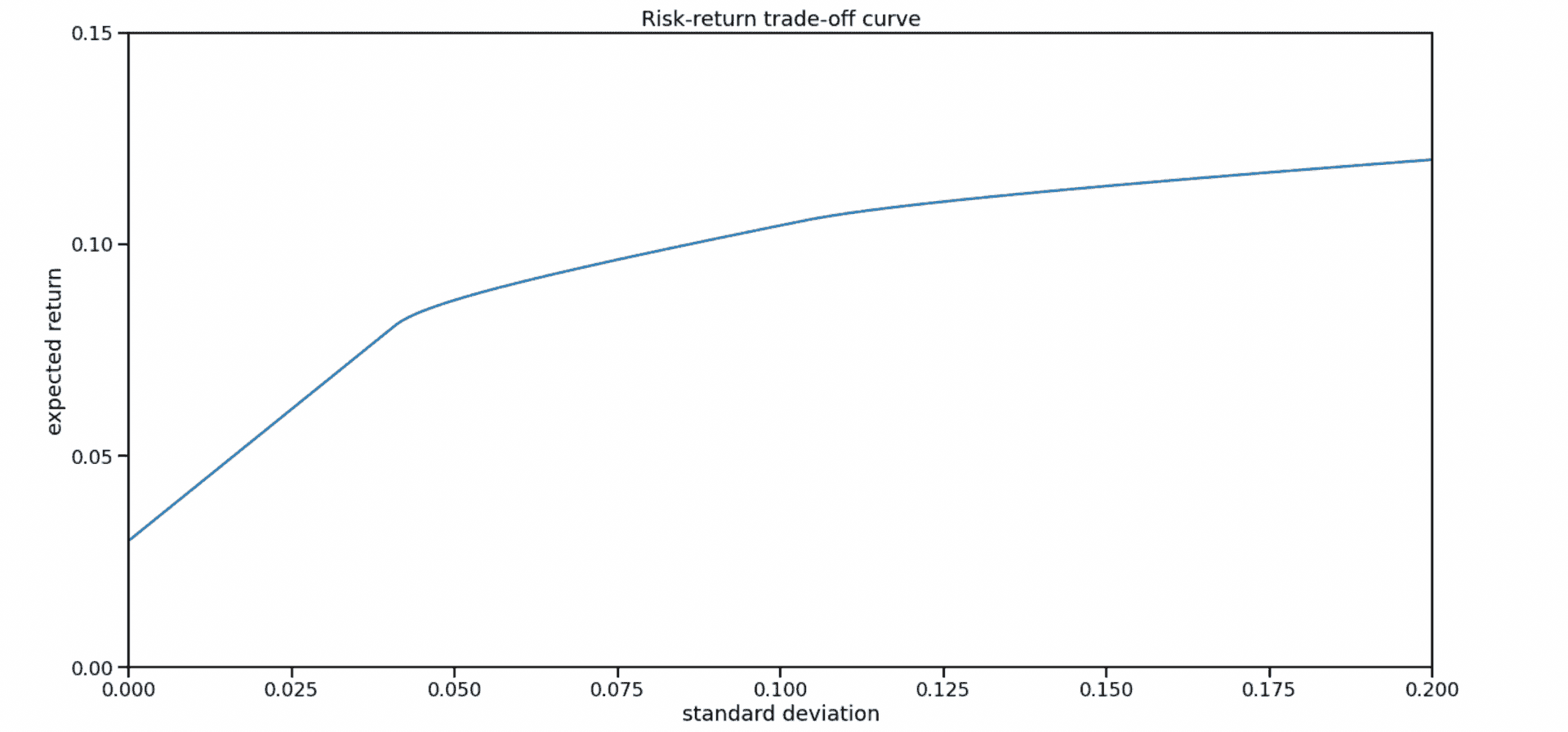
Throughout the 2020-21 pandemics the M2 money supply of the majority of European currencies exploded by 20-25%, of US dollar - by whopping 40%! Interest rates on investment-grade bonds are negligible compared to that, and they no longer serve their purpose as the primary conservative investment (3% interest is not any good, if the body of the bond looses 10-20% of its value a year because of the excessive money creation). Thus, a conservative investor has to go for a diversified portfolio of stocks, which can be constructed in the framework of the Modern Portfolio Theory - a trivial application of linear algebra and numeric optimization (oh, I meant, artificial intelligence, what am I saying). And as they say in Russia, the difference between theory and practice is that in theory there is no difference, while in practice there is some.

How does DeepMind AlphaFold2 work?
 December 25, 2021 30 min read

I believe that DeepMind AlphaFold2 and Github Co-pilot were among the most prolific advances of technology made in 2021. Two years after their initial breakthrough, DeepMind released the second version of their revolutionary system for protein 3D structure prediction. This time they basically solved the 3D structure prediction problem that held for more than 50 years. These are the notes from my detailed talk on the DeepMind AlphaFold2 system.

Quadratic programming
 December 06, 2021 5 min read

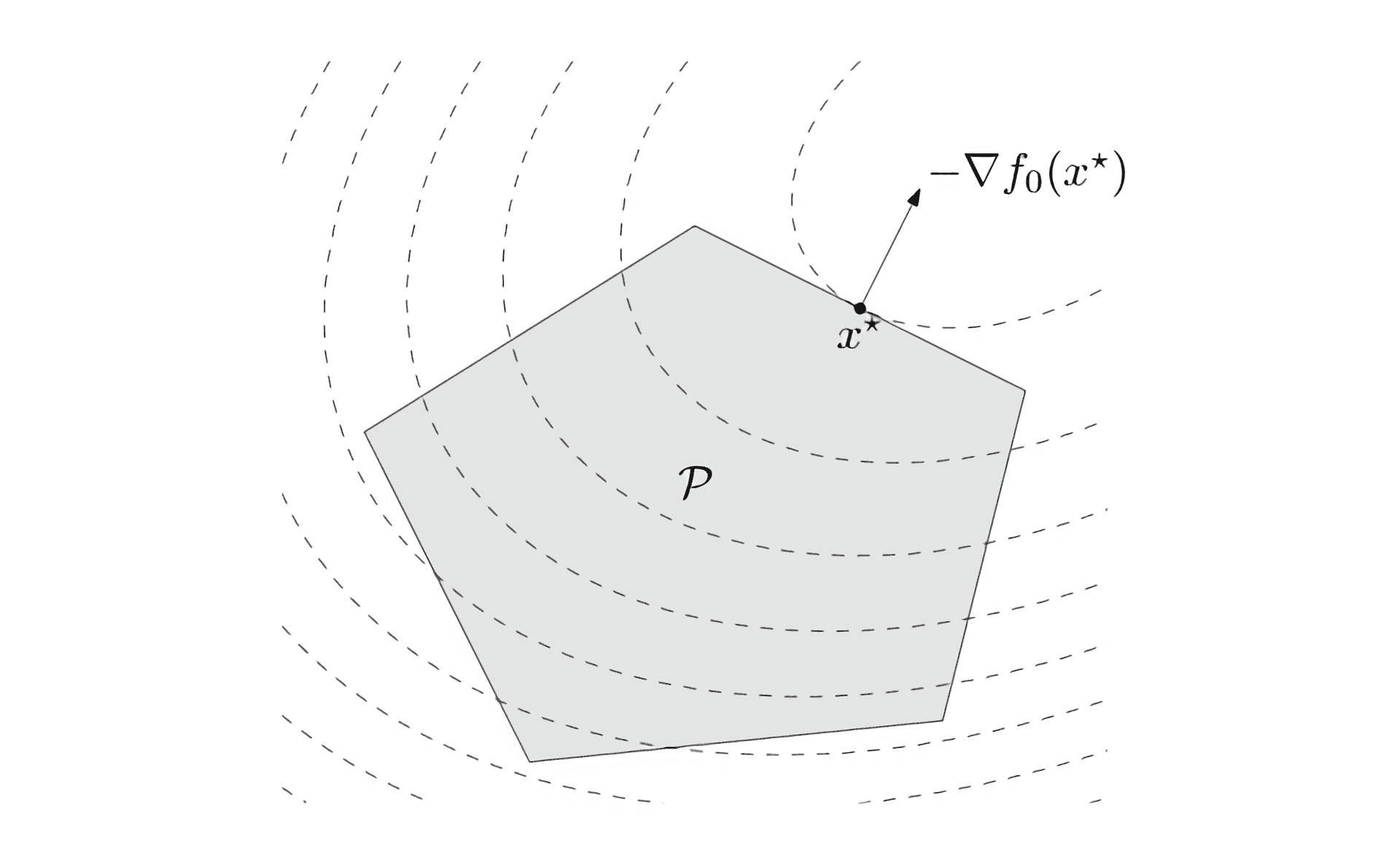
Solution of quadratic programming problem in polynomial time by Soviet mathematicians in the late 1970s - early 1980s paved the way for several important machine learning methods of 1990s, such as Lasso/ElasticNet regression (with its L1 regularization) and Support Vector Machines (SVM). These methods are incredibly useful, because they produce sparse solutions, effectively serving as a proxy for L0 regularization, in feature space/data point space respectively. Thanks to QP magic, they manage to do this in polynomial time, while straightforward application of L0 norm is NP-hard and cannot be done efficiently.

Overview of consensus algorithms in distributed systems - Paxos, Zab, Raft, PBFT
 October 03, 2021 17 min read

The field of consensus in distributed systems emerged in late 1970s - early 1980s. Understanding of consensus algorithms is required for working with fault-tolerant systems, such as blockchain, various cloud and container environments, distributed file systems and message queues. To me it feels like consensus algorithms is a rather pseudo-scientific and needlessly overcomplicated area of computer science research. There is definitely more fuzz about consensus algorithms than there should be, and many explanations are really lacking the motivation part. In this post I will consider some of the most popular consensus algorithms in the 2020s.

Популярная статья о распределенных вычислительных системах, блокчейне и криптографии в контексте выборов
 September 25, 2021 22 min read

В контексте прошедших выборов многие люди, не являющиеся техническими специалистами, заинтересовались тематикой блокчейна, криптографии и т.п. Меня попросили подготовить популярную статью на эту тему.

Divergence, Gauss-Ostrogradsky theorem and Laplacian
 September 20, 2021 9 min read

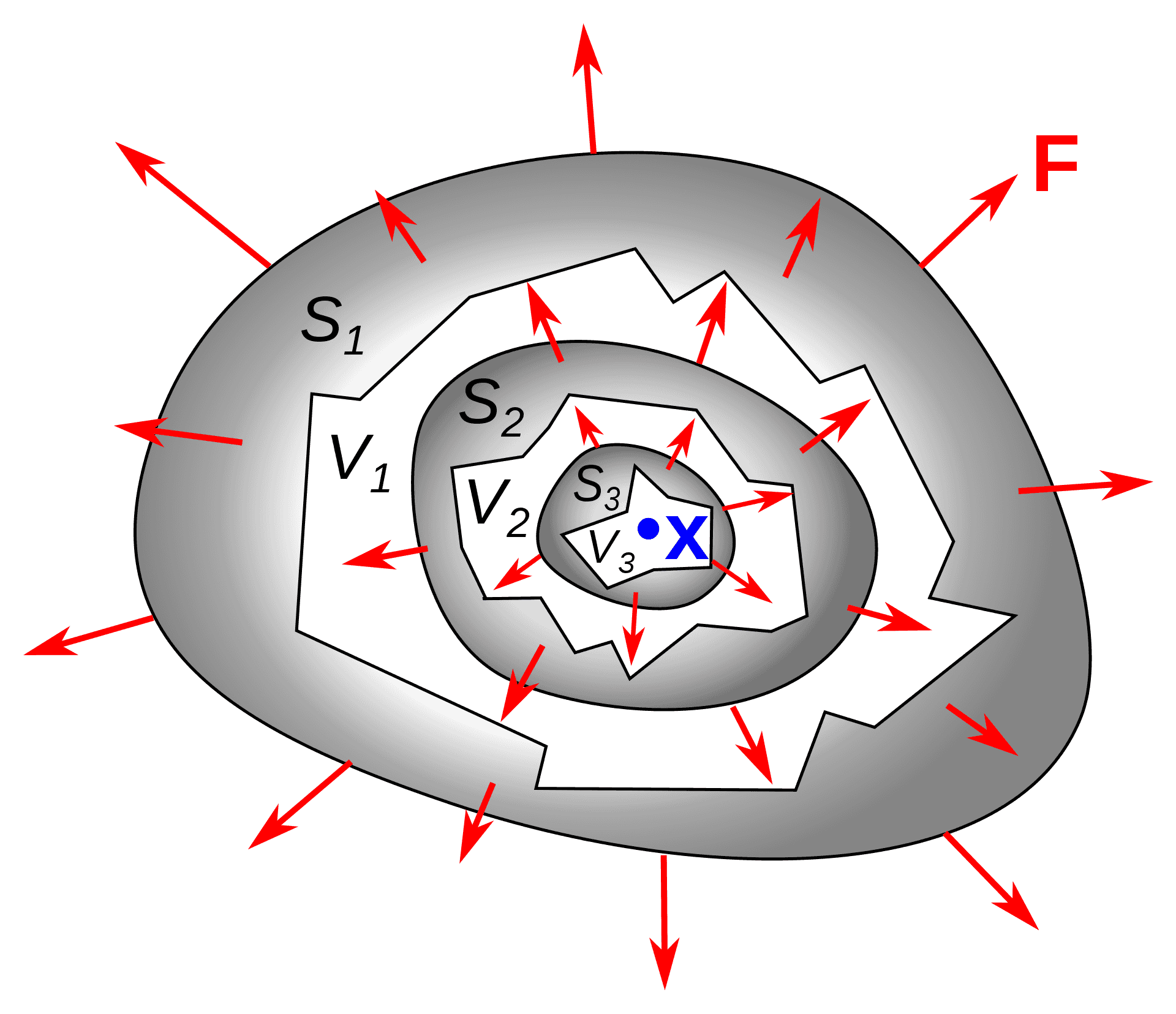
Laplacian is an interesting object that initially was invented in multivariate calculus and field theory, but its generalizations arise in multiple areas of applied mathematics, from computer vision to spectral graph theory and from differential geometry to homologies. In this post I am going to explain the intuition behind Laplacian, which requires the introduction of the notion of divergence first. I'll also touch the famous Gauss-Ostrogradsky theorem.

Johnson-Lindenstrauss lemma
 September 10, 2021 14 min read

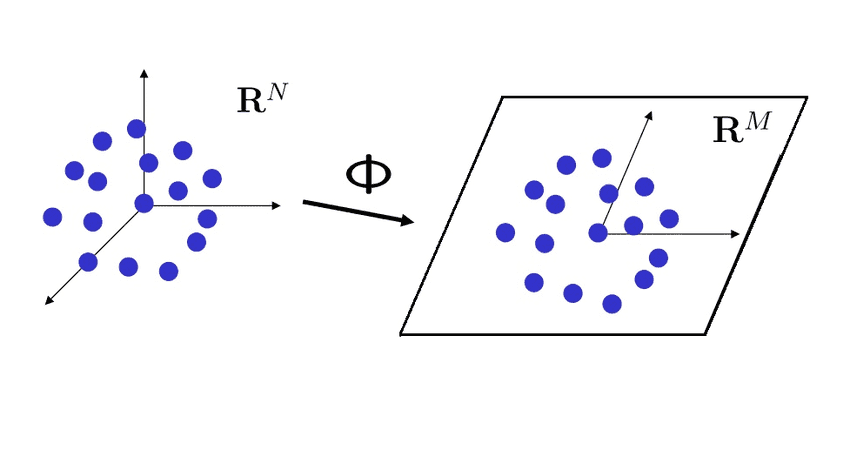
Johnson-Lindenstrauss lemma is a super-important result on the intersection of fields of functional analysis and mathematical statistics. When you project a dataset from multidimensional space to a lower-dimensional one, it allows you to estimate, by how much you distort the distances upon projection. In this post I work out its proof and discuss applications.

Intro to spectral graph theory
 September 02, 2021 3 min read

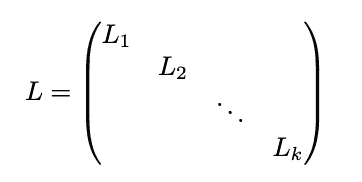
Spectral graph theory is an amazing connection between linear algebra and graph theory, which takes inspiration from multivariate calculus and Riemannian geometry. In particular, it finds applications in machine learning for data clustering and in bioinformatics for finding connected components in graphs, e.g. protein domains.

Singular Value Decomposition
 August 26, 2021 10 min read

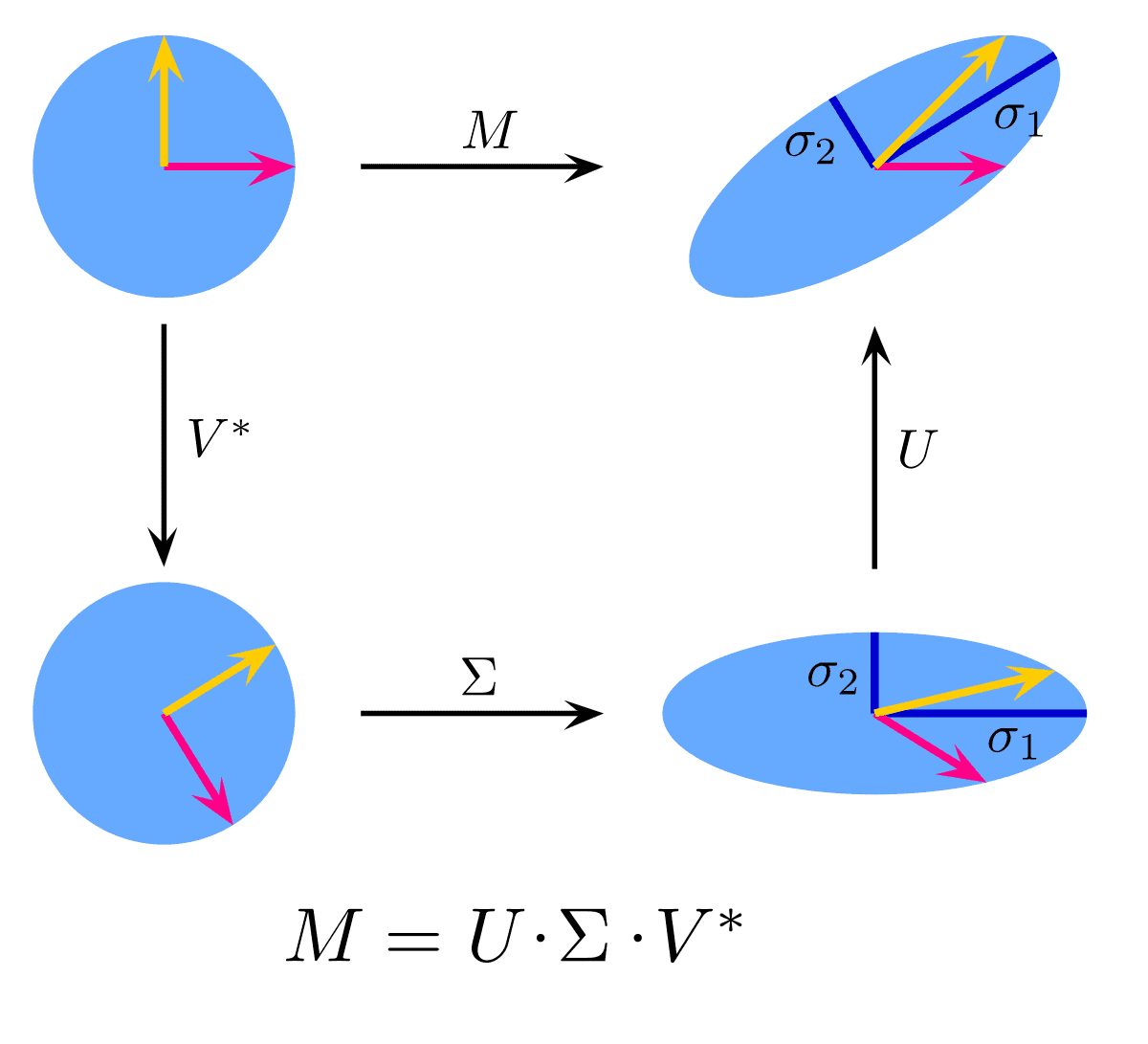
Singular value decomposition is a way of understanding a rectangular (i.e. not necessarily square) matrix from the operator norm standpoint. It is complementary perspective to eigenvalue decomposition that finds numerous application in statistics, machine learning, bioinformatics, quantum computers etc. This post explains its nature and connections to operator norm, least squares fitting, PCA, condition numbers, regularization problems etc.

Condition numbers
 August 23, 2021 7 min read

The notion of condition numbers arises when you are studying the problem of numeric stability of solutions of ordinary linear equations systems (OLES). This concept is really important in such practical applications as least-squares fitting in regression problems or search of inverse matrix (which can be an inverse of covariance matrix in such machine learning applications as Gaussian processes). Another example of their use is the time complexity of quantum algorithms for solving OLES - complexity of those algorithms is usually a polynomial or (poly-) logarithmic function of condition numbers. This post gives a brief review of condition numbers.

Normal matrices - unitary/orthogonal vs hermitian/symmetric
 August 13, 2021 8 min read

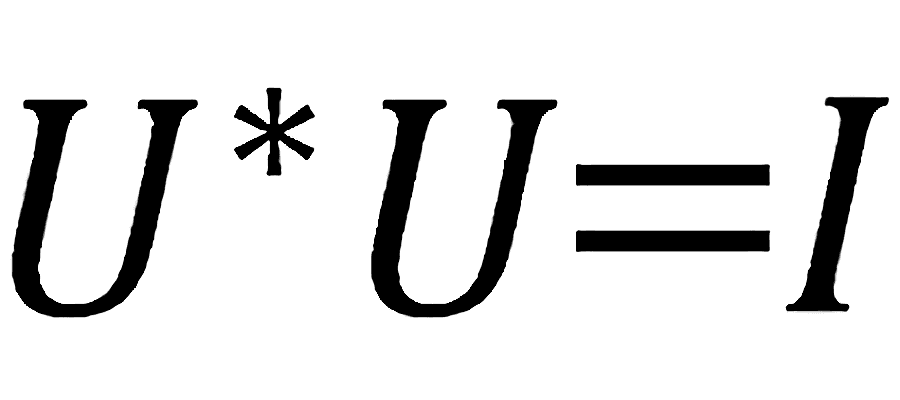
Both orthogonal and symmetric matrices have orthogonal eigenvectors matrices. If we look at orthogonal matrices from the standpoint of outer products, as they often do in quantum mechanics, it is not immediately obvious, why they are not symmetric. The demon is in complex numbers - for symmetric matrices eigenvalues are real, for orthogonal they are complex.

Kernel methods and Reproducing Kernel Hilbert Space (RKHS)
 August 03, 2021 38 min read

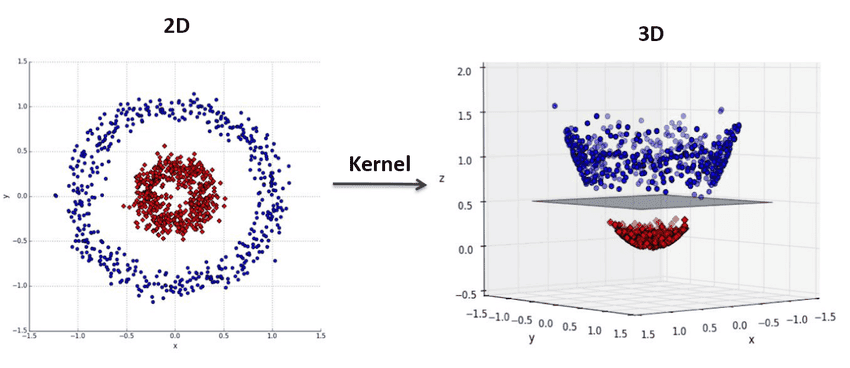
Kernel methods are yet another approach to automatic feature selection/engineering in the machine learning engineer's toolbox. It is based on theoretical results from the field of functional analysis, dating to 1900s and 1950s, called Reproducing Kernel Hilbert Space. Kernel methods, such as kernel SVMs, kernel ridge regressions, gaussian processes, kernel PCA or kernel spectral clustering are very popular in machine learning. In this post I'll try to summarize my readings about this topic, linearizing the pre-requisites into a coherent story.

Roadmap to understanding the quantum mechanics
 July 16, 2021 2 min read

In my university days I used to attend a course of quantum chemistry/mechanics, which was given in a typical post-soviet education style. All formalism, no essentials. As quantum computers are getting closer and closer to the reality by the day, I had a practical reason to finally improve my understanding of the theory. Here is my roadmap to understanding the quantum mechanics.

Wishart, matrix Gamma, Hotelling T-squared, Wilks' Lambda distributions
 July 13, 2021 4 min read

In this post I'll briefly cover the multivariate analogues of gamma-distribution-related univariate statistical distributions.

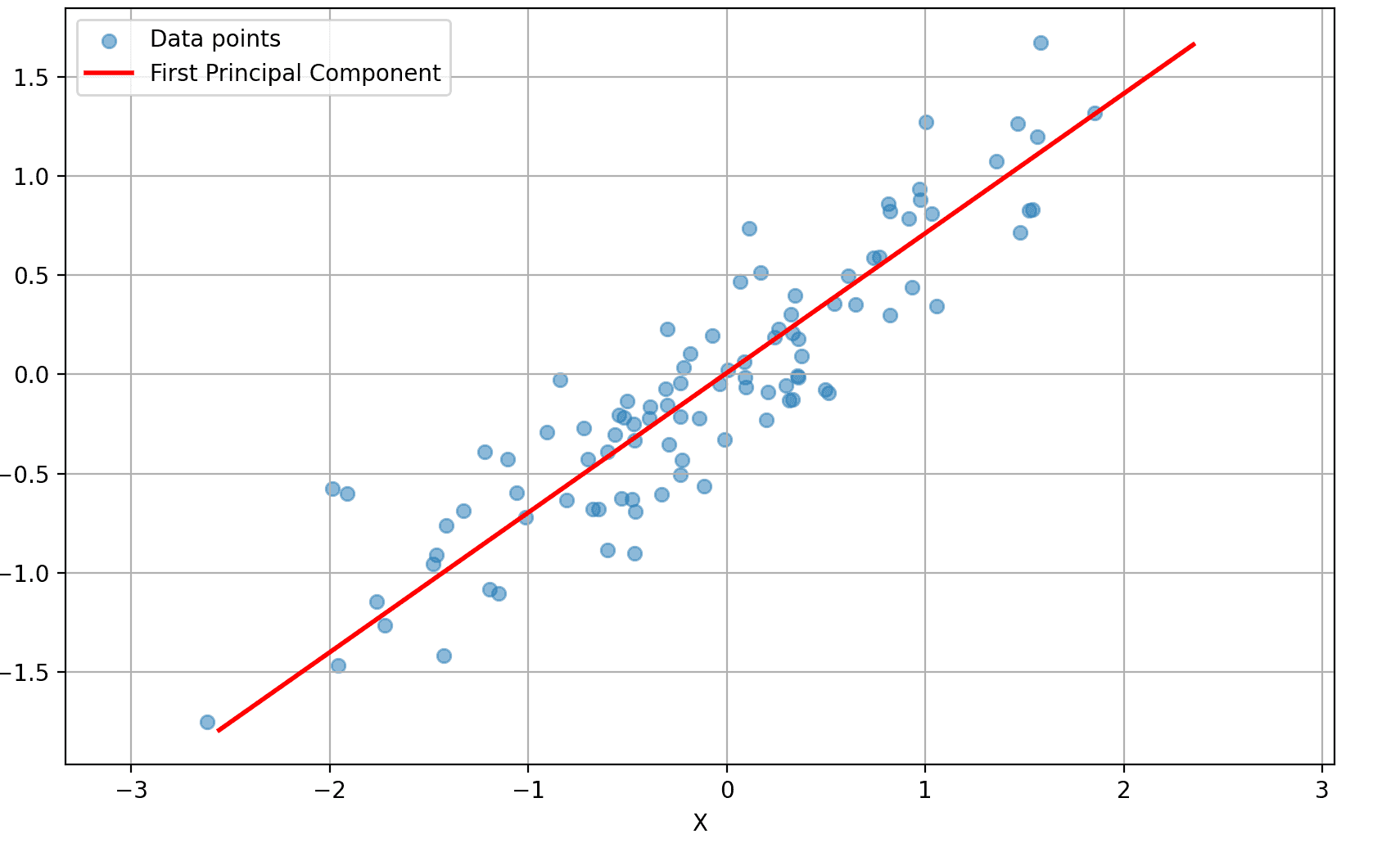
Principal components analysis
 July 12, 2021 6 min read

Principal components analysis is a ubiquitous method of dimensionality reduction, used in various fields from finance to genomics. In this post I'm going to consider PCA from different standpoints, resulting in various perspectives on it.

Beta distribution and Dirichlet distribution
 July 10, 2021 6 min read

Beta distribution and Dirichlet distribution are Bayesian conjugate priors to Bernoulli/binomial and categorical/multinomial distributions respectively. They are closely related to gamma-function and Gamma-distribution, so I decided to cover them next to other gamma-related distributions.

Multivariate normal distribution
 July 01, 2021 18 min read

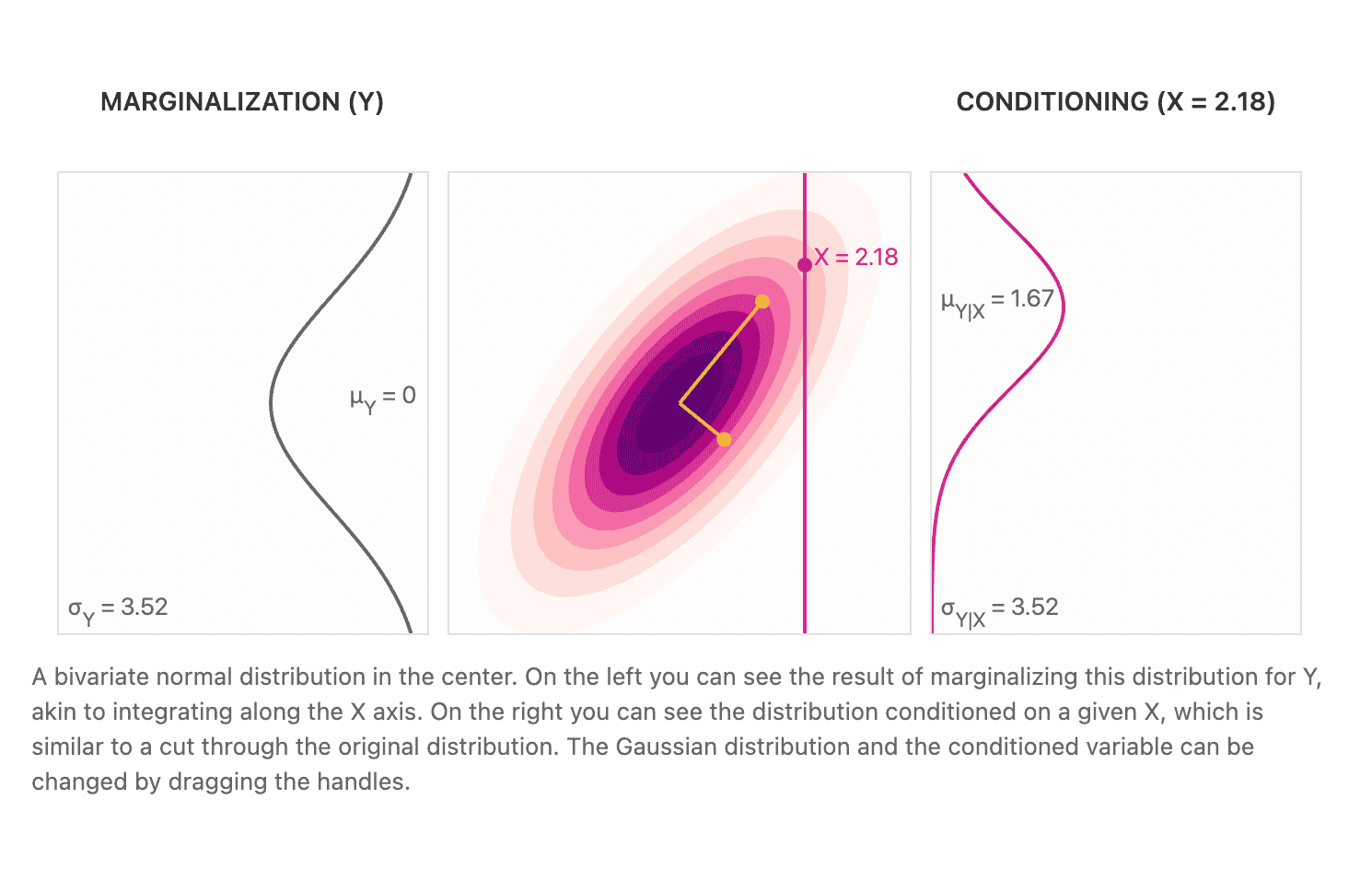
Multivariate normal distribution arises in many aspects of mathematical statistics and machine learning. For instance, Cochran's theorem in statistics, PCA and Gaussian processes in ML heavily rely on its properties. Thus, I'll discuss it here in detail.

Cochran's theorem
 June 30, 2021 17 min read

Here I discuss the Cochran's theorem that is used to prove independence of quadratic forms of random variables, such as sample variance and sample mean.

Student's t-distribution, t-test
 June 20, 2021 13 min read

Here I discuss, how to derive Student's t-distribution, an important statistical distribution, used as a basis for t-test.

Snedecor's F distribution and F-test
 June 19, 2021 12 min read

Here I discuss, how to derive F distribution as a random variable, which is a ratio of two independent chi-square disributions. I'll also briefly discuss F-test and ANOVA here.

Pearson's Chi-square test - intuition and derivation
 June 17, 2021 23 min read

Here I discuss, how an average mathematically inclined person like myself could stumble upon Karl Pearson's chi-squared test (it doesn't seem intuitive at all from the first glance). I demonstrate the intuition behind it and then prove its applicability to multinomial distribution.

Survival analysis - survival function, hazard rate, cumulative hazard rate, hazard ratio, Cox model
 June 11, 2021 7 min read

Here I discuss the statistics apparatus, used in survival analysis and durability modelling.

Data structures for efficient NGS read mapping - suffix tree, suffix array, BWT, FM-index
 June 10, 2021 3 min read

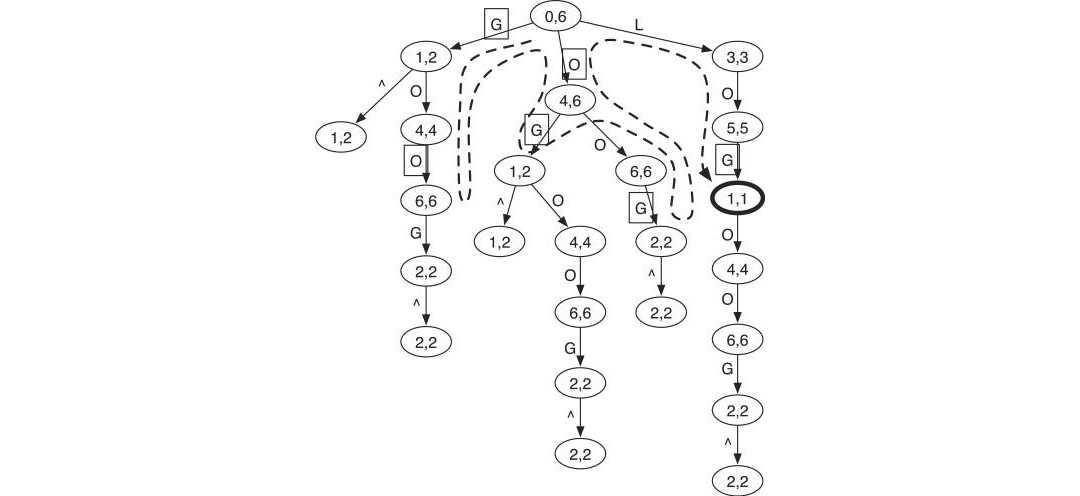
In Next-Generation Sequencing bioinformatics there is a problem of mapping so-called reads - short sequences of ~100 nucleotides - onto a full string that contains them - the reference genome. There is a number of clever optimizations to this process, which I consider in this post.

Gamma, Erlang, Chi-square distributions... all the same beast
 June 09, 2021 19 min read

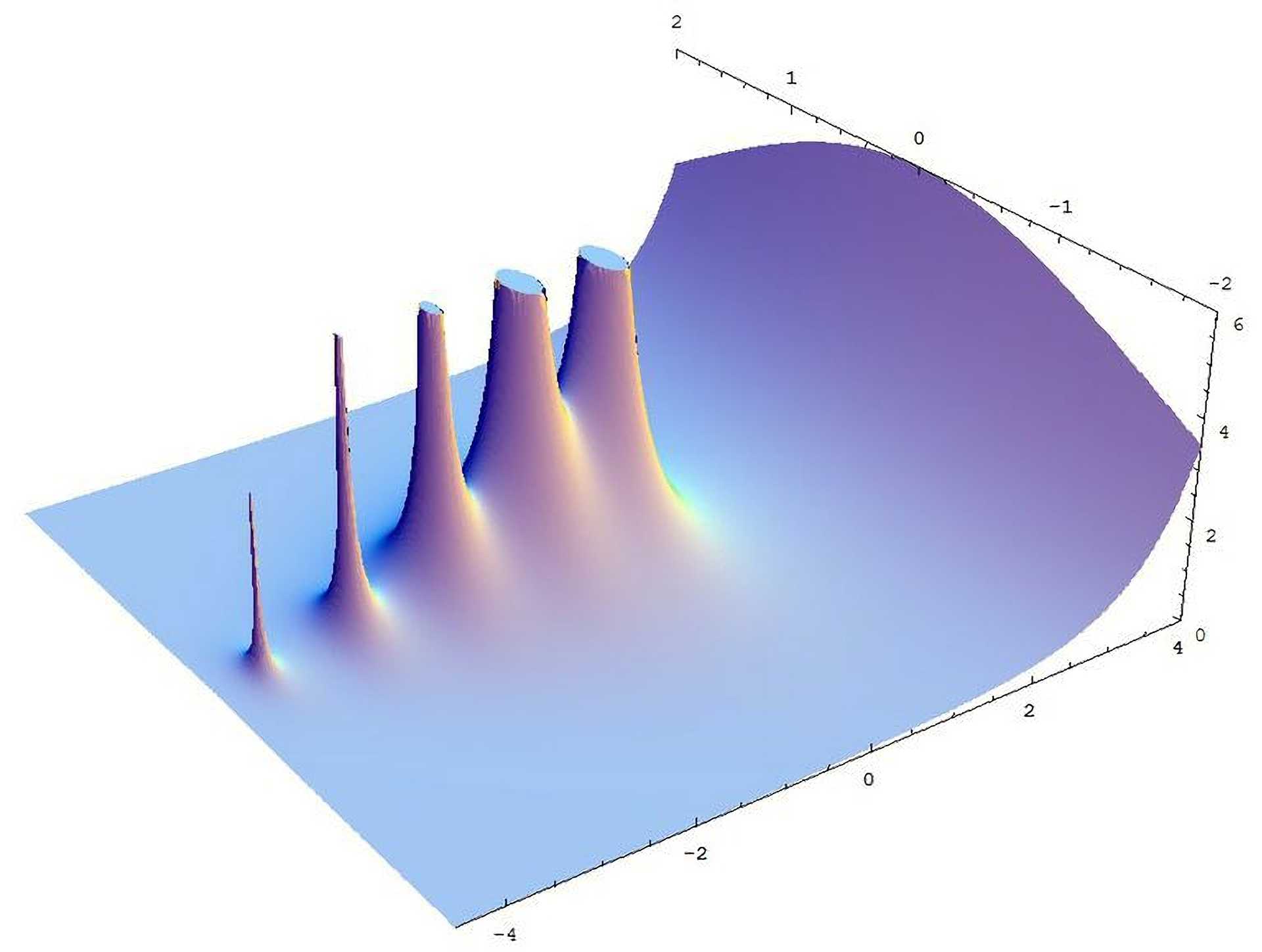
Probably the most important distribution in the whole field of mathematical statistics is Gamma distribution. Its special cases arise in various branches of mathematics under different names - e.g. Erlang or Chi-square (and Weibull distribution is also strongly related) - but essentially are the same family of distribution, and this post is supposed to provide some intuition about them.

Why Huffman trees require a bottom-up walk to be optimal?
 June 08, 2021 1 min read

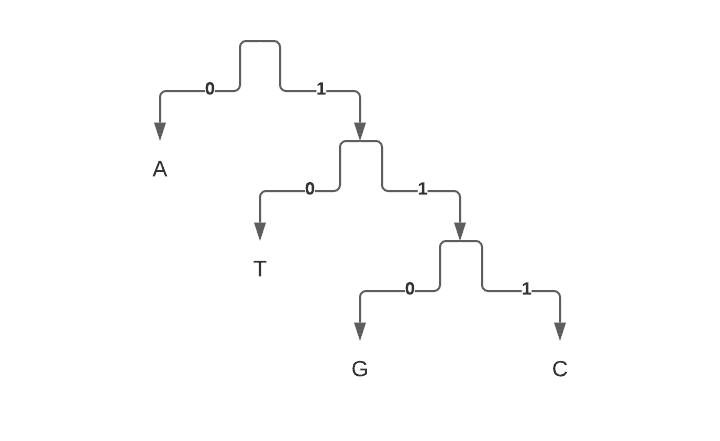
Why greedy algorithm wouldn't work for Huffman trees?

A case study of 20PiB Ceph cluster with 100GB/s throughput
 March 15, 2021 11 min read

Recently we deployed a Ceph cluster that might be one of the more powerful in Russia in terms of both throughput and storage capacity. I'd like to discuss nuts and bolts of that system in this post.

Blog version 4
 July 13, 2019 1 min read

I just released a new version of my personal blog http://borisburkov.net, this time powered by Gatsby.js.

Asyncio ecosystem
 March 29, 2019 3 min read

I have a very bad developer experience with Asyncio. It is such a messy and overcomplicated system that I studied it over at least 3 times now. I figured, it's time to cut my losses and write a post about it!

Екатерина Шульман - лекция о российском социуме
 March 15, 2019 2 min read

В сентябре мы с Андреем Попеску, Артемом Ломакиным и Женей Галимовым ели пиццу, лениво разглядывали задачки на Кеггле и трепались о разном. Спустя пару недель я сбросил в наш чатик лекцию Екатерины Шульман о влиянии АИ на социум.

Манчестер - хлопок и паровозы
 February 27, 2019 3 min read

Подобно тому, как между современными инженерами из IBM, Google и Ригетти сейчас развернулась гонка за то, чтобы первыми достичь квантового превосходства, первые инженеры начала 19-ого соревновались в том, кому удастся произвести первый паровоз массового производства, который должен был курсировть между Манчестером и Ливерпулем.

DeepMind - Презентация AlphaFold в EBI
 February 07, 2019 4 min read

Два месяца назад весь мир облетела новость, что DeepMind выиграл известное соревнование по предсказанию 3D-структур белков CASP, порвав всех биоинформатиков с впечатляющим отрывом. Многие люди из мира биотеха теперь пытаются осознать, 'что это было'? Революция или эволюция, наука или инженерия, талант или финансирование? Волею судеб я когда-то оказался совсем недалеко от этой области науки, поэтому потратил несколько дней чтобы разобраться в деталях - а между тем в EBI приехал наводить мосты ведущий инженер проекта Эндрю Сеньор из DeepMind.

Amazon Alexa
 February 07, 2019 4 min read

Послушал двух парней из кембриджского офиса Амазона, работающих над Алексой. Составил общее впечатление о том, каково оно - работать в Амазон.

Prowler.io
 January 22, 2019 1 min read

Побывал на презентации Prowler.io - самого модного кембриджского стартапа.

Focal loss and Average Precision
 November 12, 2018 2 min read

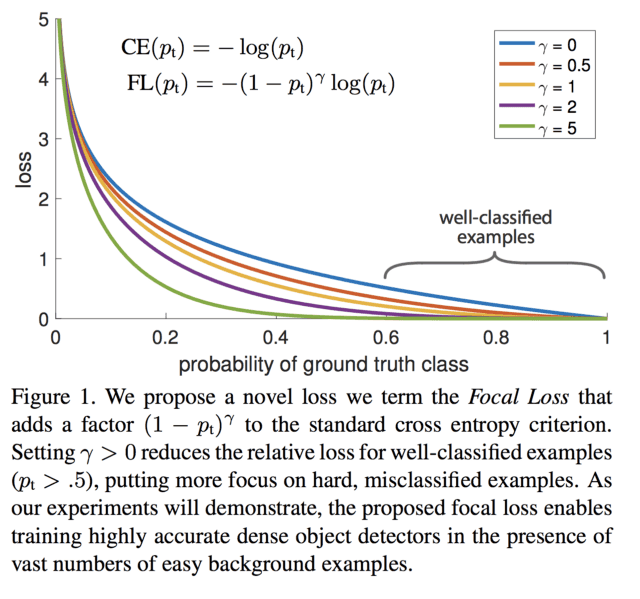
A simple loss function for multiclass classification with multiple classes that beautifully deals with class imbalance

Встреча с Обри де Греем
 November 10, 2018 1 min read

Поглядел наконец живьем на главного геронтологического оптимиста.

Карьера в империи данных - Лекция дата-инженера из Facebook
 October 23, 2018 1 min read

Этой весной на ML/AI-конференции в Microsoft Research я коротко обсудил вопрос построения карьера дата-сайнтиста в IT-компаниях с Зубином Гарамани, профессором сильнейшего инженерного факультета Кембриджа и директором лабораторий искусственного интеллекта в Убер. Зубин тогда объяснил, что от ваших научных регалий обычно зависит та позиция, на которую вы устраиваетесь на работу, и роль в компании. И вот в это воскресенье я получил подтверждение его слов от Марека Романовича, дата инженера в Фейсбуке в Нью-Йорке.

20 примеров - как и на что живут РНК-биоинформатики?
 October 19, 2018 5 min read

Только что прошел мой второй RNAcentral consortium meeting, и это было настолько интересное мероприятие с точки зрения понимания того, как устроен мир, что я не могу не поделиться этой информацией.

Postgres roles
 October 09, 2018 2 min read

Postgres authentication and permission system sometimes feels like a total mess to me. This is a recap of how it works.

Docker users and user namespaces
 October 09, 2018 1 min read

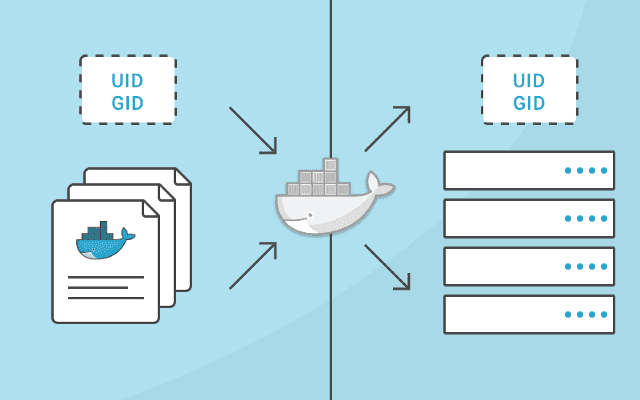
After taking a break from DevOps for a few months and switching to other fields, I would always forget the details of how users within a docker container map to users on the host machine. This is a condensed recap of user mappings that should save me time, upon switching the contexts.

Почему образование в США с 1985 по 2013 подорожало в 6 раз?
 February 02, 2018 7 min read

Это краткий пересказ замечательной главы из книги Кэти О'Нил "Weapons of Math Destruction", посящённой тому, как большие данные углубляют социальное неравенство, концентрируют власть в руках капиталистов и делают обычного человека всё более беспомощным.

Мир МедТеха
 January 23, 2018 6 min read

В конце прошлой недели я был на хакатоне по медицинской технике и получил массу знаний и впечатлений. Это совершенно другой мир, который живёт под девизом "Health & Wealth" и держится на патентах и контактах.

OpenStack, Kubernetes and OpenShift crash course for impatient - Kubernetes
 January 20, 2018 2 min read

Kubernetes is a system for orchestration of containerized applications that can be used to deploy your microservice-based websites to the cloud. Kubernetes is created by Google, based on their internal orchestration system Borg (although, codebase is re-written completely from scratch). Kubernetes is written mostly in Go programming languages and is open-source.

OpenStack, Kubernetes and OpenShift crash course for impatient - OpenStack
 January 19, 2018 1 min read

OpenStack is a pretty old standard for describing cloud resources and interacting with them. Most of its APIs were suggested around 2012. It is "Open" because multiple vendors that provide cloud services (including Rackspace and Red Hat) agreed to use the same API for interaction with them and called it OpenStack.

OpenStack, Kubernetes and OpenShift crash course for impatient - introduction
 January 18, 2018 2 min read

Much like a junkie from a russian anecdote, who started shouting "Jiggers, cops!" when they brought him to the police station, EBI in 2018 suddenly discovered the existence of cloud technologies.

Traction
 December 17, 2017 54 min read

MOST STARTUPS DON'T FAIL BECAUSE THEY CAN'T BUILD THE PRODUCT. MOST STARTUPS FAIL BECAUSE THEY CAN'T GET TRACTION.

BurkovBA.github.io is online!
 December 14, 2017 3 min read

I've been procrastinating over my blog for almost a year. Initially I wrote it in Angular in early 2017 and re-wrote everything in React in the last couple of weeks. At last, following Github's "ship early - ship often" motto, I shipped it today. Probably the most challenging aspect of the whole work was to make Github pages play nice with React SPA - I'll tell you how in this post.

Энигма, часть 5 - "Бисмарк" и "дебютантка"
 November 30, 2017 2 min read

В ходе "Битвы за Атлантику" в 41-ом году немецкий флот пытался отрезать Великобританию от морского сообщения с континентом и Штатами. У немцев было превосходство в военно-морском флоте, и на какое-то время им даже удалось установить вокруг островов морскую блокаду.

Back in Black - Памяти Малькольма Янга
 November 21, 2017 3 min read

В течение последнего месяца умерли двое австралийских музыкантов - братья Джордж и Малькольм Янги. Если смерть Джорджа была мало кем замечена, то про Малькольма Янга сообщали во всех СМИ, ведь он - основатель легендарной австралийской рок-группы AC/DC."

Энигма, часть 1 - Что такое "Энигма"?
 November 01, 2017 2 min read

Что вообще такое эта знаменитая "Энигма", которую все так стремились взломать, и зачем она была нужна?

Энигма, часть 0 - Британия во Второй мировой
 October 25, 2017 1 min read

Прежде чем перейти собственно к теме повествования, криптографии и Блетчли-парк, я хотел сказать пару слов об участии Британии в войне - чтобы дать контекст.

Энигма. Анонс
 October 21, 2017 1 min read

Все смотрели "Игру в Имитацию"? Камбербетч, конечно, прекрасен, а в жизни, конечно, всё было не так. Этот пост про математиков и инженеров из GC&CS (Government Code and Cypher School) во главе с Аланом Тьюрингом, нашедших уязвимости в немецких шифровальных машинах "Энигма" и "Лоренцå" во Вторую мировую войну, и спасших тем самым десятки или даже сотни тысяч соотечественников.

Facebook license
 September 25, 2017 2 min read

Несколько дней назад Facebook изменил лицензии ряда самых популярных своих open-source библиотек React, Flow, Jest и Immutable.js на стандартную MIT.

Congenica
 September 21, 2017 4 min read

Вчера был на семинаре основателей Congenica - компании, занимающейся медицинской генетикой врождённых болезней. Выступали двое из пяти или шести её основателей Ник Ленч и Энди Ричардс, и самое мощное впечатление произвёл Ричардс, с которым я после этого побеседовал.

Babraham Institute
 July 05, 2017 1 min read

Как устроена жизнь простого российского мол. биолога я примерно представляю. Денег нет - денег нет - денег нет - денег нет - да ну нафиг, пойду в Мерк... \n Посмотрел, как она устроена у английского. В каком-то смысле совсем по-другому, в каком-то - точно так же...

Об овцах и стартапщиках
 January 05, 2017 3 min read

Гербом Англии должны быть не три льва, а дюжина овец. Этим кротким созданиям она во-многом обязана своей индустриальной мощью, позволившей ей так вырваться вперед в общественном и экономическом развитии.